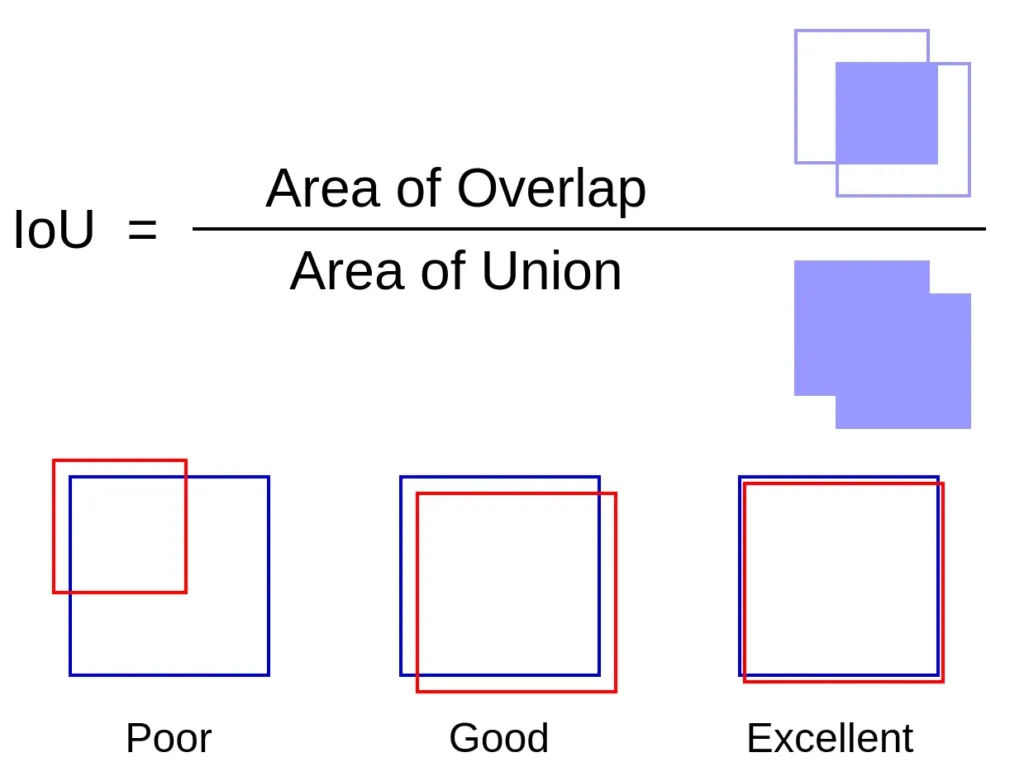
Intersection over Union (IoU) is a popular evaluation metric used in the field of computer vision and object detection. It is used to calculate the overlap between two bounding boxes and is used to evaluate the accuracy of object detection algorithms. IoU is a value between 0 and 1 that represents the overlap between the ground truth and predicted bounding boxes. A high IoU value indicates that the predicted bounding box is accurately aligned with the ground truth bounding box.
Intersection over Union Calculation
The IoU between two bounding boxes is calculated as the ratio of the intersection area over the union area. The intersection area is the overlapping region between the two bounding boxes, while the union area is the total area of the two bounding boxes combined.
In order to calculate the IoU between two bounding boxes, we need to find the coordinates of the intersection and union regions. The coordinates of the intersection region are given by the minimum and maximum values of the x- and y-coordinates of the two bounding boxes. The union region is the area enclosed by the minimum and maximum values of the x- and y-coordinates of the two bounding boxes.
IoU Implementation
The IoU calculation can be implemented in the python programming language using different libraries including NumPy, TensorFlow, and PyTorch.
Numpy Implementation
import numpy as np
def intersection_over_union(boxA, boxB):
# determine the (x, y)-coordinates of the intersection rectangle
x1 = max(boxA[0], boxB[0])
y1 = max(boxA[1], boxB[1])
x2 = min(boxA[2], boxB[2])
y2 = min(boxA[3], boxB[3])
# compute the area of intersection rectangle
intersection_area = max(0, x2 - x1 + 1) * max(0, y2 - y1 + 1)
# compute the area of both the prediction and ground-truth rectangles
boxA_area = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxB_area = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
# compute the intersection over union by taking the intersection
# area and dividing it by the sum of prediction + ground-truth
# areas - the interesection area
iou = intersection_area / float(boxA_area + boxB_area - intersection_area)
# return the intersection over union value
return iou
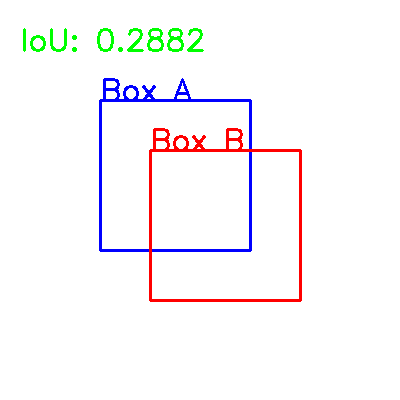
Now, let us test the above NumPy implementation of the Intersection over Union (IoU).
# Two bounding boxes
boxA = [100, 100, 250, 250]
boxB = [150, 150, 300, 300]
iou = intersection_over_union(boxA, boxB)
print("IoU: ", iou)
# A simple 400 x 400 blnk white image
image = np.ones((400, 400, 3), dtype=np.float32) * 255
# Plotting IoU on image
cv2.putText(image, f"IoU: {iou:.4f}", (20, 50), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 255, 0), 2)
# Plotting bounding box A
image = cv2.rectangle(image, (boxA[0], boxA[1]), (boxA[2], boxA[3]), (255, 0, 0), 2) ## Blue
cv2.putText(image, "Box A", (boxA[0], boxA[1]), cv2.FONT_HERSHEY_SIMPLEX, 1, (255, 0, 0), 2)
# Plotting bounding box B
image = cv2.rectangle(image, (boxB[0], boxB[1]), (boxB[2], boxB[3]), (0, 0, 255), 2) ## Red
cv2.putText(image, "Box B", (boxB[0], boxB[1]), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 0, 255), 2)
cv2.imwrite("iou.png", image)
Output:
IoU: 0.2881557018163329
TensorFlow Implementation
import tensorflow as tf
def intersection_over_union(boxA, boxB):
# determine the (x, y)-coordinates of the intersection rectangle
x1 = tf.maximum(boxA[0], boxB[0])
y1 = tf.maximum(boxA[1], boxB[1])
x2 = tf.minimum(boxA[2], boxB[2])
y2 = tf.minimum(boxA[3], boxB[3])
# compute the area of intersection rectangle
intersection_area = tf.maximum(0, x2 - x1 + 1) * tf.maximum(0, y2 - y1 + 1)
# compute the area of both the prediction and ground-truth rectangles
boxA_area = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxB_area = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
# compute the intersection over union by taking the intersection
# area and dividing it by the sum of prediction + ground-truth
# areas - the interesection area
iou = intersection_area / (boxA_area + boxB_area - intersection_area)
# return the intersection over union value
return iou
boxA = [100, 100, 250, 250]
boxB = [150, 150, 300, 300]
iou = intersection_over_union(boxA, boxB)
print("IoU: ", iou)
Output:
IoU: tf.Tensor(0.2881557018163329, shape=(), dtype=float64)
PyTorch Implementation
import torch
def intersection_over_union(boxA, boxB):
# determine the (x, y)-coordinates of the intersection rectangle
x1 = torch.max(boxA[0], boxB[0])
y1 = torch.max(boxA[1], boxB[1])
x2 = torch.min(boxA[2], boxB[2])
y2 = torch.min(boxA[3], boxB[3])
# compute the area of intersection rectangle
intersection_area = torch.max(torch.tensor(0.0), x2 - x1 + 1) * torch.max(torch.tensor(0.0), y2 - y1 + 1)
# compute the area of both the prediction and ground-truth rectangles
boxA_area = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxB_area = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
# compute the intersection over union by taking the intersection
# area and dividing it by the sum of prediction + ground-truth
# areas - the interesection area
iou = intersection_area / (boxA_area + boxB_area - intersection_area)
# return the intersection over union value
return iou
boxA = torch.tensor([100, 100, 250, 250])
boxB = torch.tensor([150, 150, 300, 300])
iou = intersection_over_union(boxA, boxB)
print("IoU: ", iou)
Output:
IoU: tensor(0.2882)
Applications of Intersection over Union
IoU is widely used in the field of object detection. It is used in evaluating the performance of object detection algorithms. The metric can be used to measure the accuracy of an algorithm in detecting objects in an image. The IoU metric is used in a number of computer vision challenges, such as the Pascal VOC and Microsoft COCO challenges.
In real-world object detection applications, it is common to have multiple objects in a single image. In such scenarios, IoU can be used to evaluate the overlap between the prediction bounding box and the ground-truth bounding box for each object. The higher the IoU, the more accurate the prediction is.
IoU Thresholds
In object detection, IoU threshold values are used to determine if a prediction is considered a true positive, false positive, true negative, or false negative. A common IoU threshold used in object detection is 0.5. A prediction is considered a true positive if its IoU with the ground-truth bounding box is greater than 0.5, and a false positive if its IoU is less than 0.5.
In practice, the choice of the IoU threshold value depends on the specific application and the desired trade-off between precision and recall. For instance, in some applications, a high precision is preferred, and in such cases, a lower IoU threshold is used. On the other hand, in applications where recall is more important, a higher IoU threshold may be used.
Conclusion
In conclusion, Intersection over Union (IoU) is a widely used evaluation metric in the field of object detection. It is used to measure the accuracy of an object detection algorithm by calculating the overlap between the prediction bounding box and the ground-truth bounding box. The IoU metric is used in many computer vision challenges, and it can be implemented in a number of programming languages, including NumPy, TensorFlow, and PyTorch. The choice of the IoU threshold value depends on the specific application and the desired trade-off between precision and recall.